题目描述

给定一个n×n的正方形，现在你在正方形的左下角，每次你可以顺时针走n+1单元的距离，求多少次之后你可以回到起点。

例如有如下正方形，边长n=4。

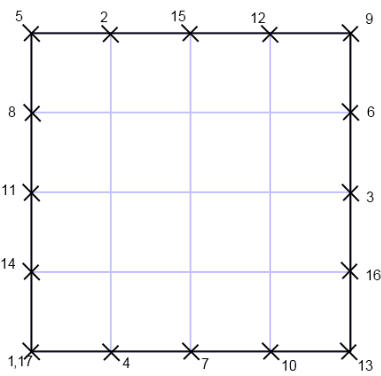
从左下角出发，标记为1，然后顺时针走n+1=5个单位走到2位置，最终走17次再次回到起点。

 

 输入

多组数据，每一行为一组数据

每一行一个整数n，代表正方形的边长(1 <= n <= 10^9)。

输出

每组输出最少需要的次数。

样例输入

4

8

100

样例输出

17

33

401

 

PS：此题，就是找规律，如果用模拟的话，超时，绝对超时。

规律：("->"代表输出)

情况一:偶数              情况二：奇数

2->9                         ①  1->2      ② 3->3

4->17                            5->10          7->7

6->25                            9->18         11->11

8->33

 

偶数 n%2==0：4*n+1

奇数  ((n-1)/2)%2==0 : n*2+1

         ((n-1)/2)%2==1: n+1

千万别忘记+1，起始点也要加上去（die在这里，自己没看清题目，枯了）

 

 

以下为模拟，超时超时超时    

#include
     
      using namespace std;int main(){    __int64 n;    while(cin>>n)    {        __int64 s=1,flag=0;        while(1)        {            s+=(n+1);            if(s>4*n)s%=(4*n);flag++;            if(s==1) break;                     }        flag=flag+1;//原点要加上去         cout<<"* "<
      
       <
      
     

 

AC代码：

#include
     
      using namespace std;int main(){    __int64 n ;    while(cin>>n)    {        if(n%2==0) cout<